Tp 1 - Extensométrie - DUT GMP2

Etude bidimensionnelle des contraintes planes à la surface d'une poutre

Présentation

On étudie la répartition des contraintes sur la surface d'une poutre sollicitée en flexion et en torsion. Une rosette de 3 jauges à 45^o est collée sur la poutre. Le matériau est élastique, linéaire, homogène et isotrope. Le module d'Young E vaut E=7,2.10¹⁰Pa. Le coefficient de Poisson ν vaut 0,3. Le facteur de jauge est 2,2.

Les trois chargements suivant sont appliqués successivement:

*3 cas d'étude*
	Cas 1	Cas 2	Cas 3
point B, F₁	10N	0	10N
point C, F₂	0	10N	10N

Pour chaque chargement, on mesure les allongements des 3 jauges de la rosette. On en déduit finalement l'état de contrainte à la surface de la pièce pour chaque chargement.

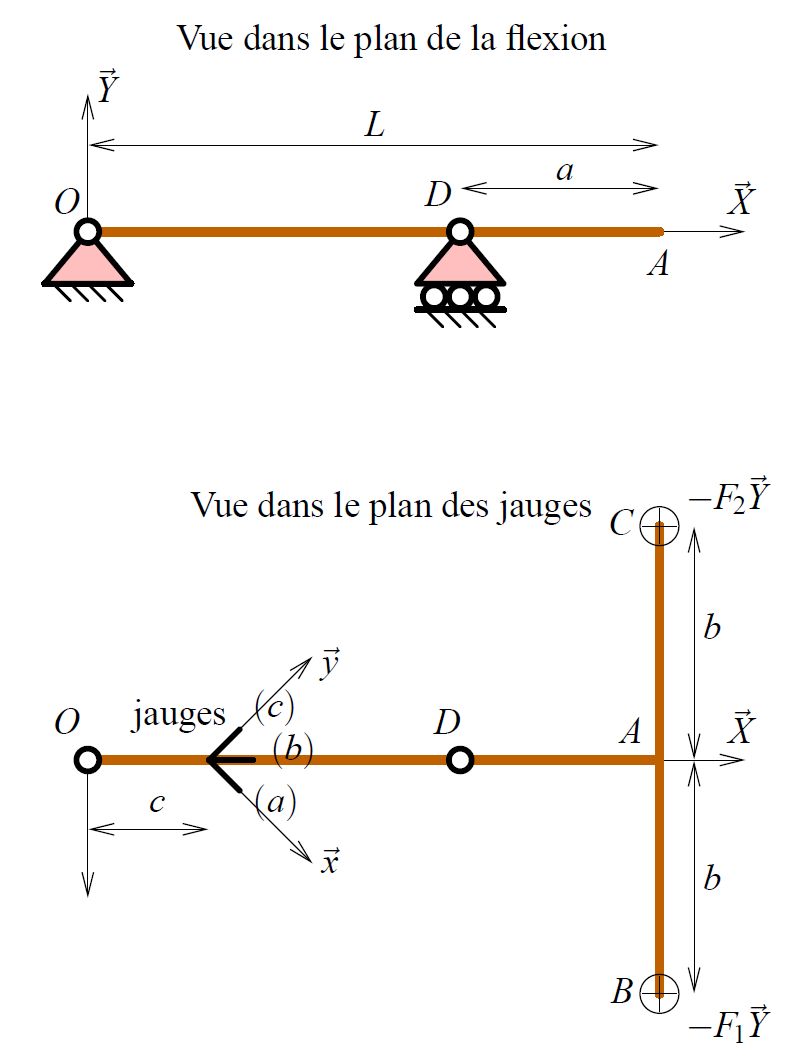
La poutre est supposée posée sur 2 appuis simples en O et D.

Etude préliminaire à rendre avant le TP

Donner en fonction de F₁, F₂ et b le torseur équivalent des actions extérieures à la poutre en A. En déduire le type de chargement correspondant à chaque cas.
Ecrire l'équilibre de la poutre afin de trouver les torseurs des efforts des liaisons écrit sous la forme:
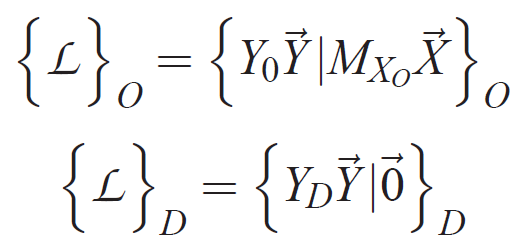
Déterminer le torseur de cohésion au niveau des jauges.
En déduire les contraintes de torsion et de flexion au niveau des jauges.
Donner l'opérateur des déformations planes au point de mesure en fonction des allongements mesurés λ_a, λ _b, λ_c des 3 jauges dans une base (x,y) locale aux 3 jauges.
Donner l'expression de l'opérateur des contraintes planes en fonction des composantes de l'opérateur des déformations, du module d'Young et du coefficient de Poisson.

Mesures

Mesurer les déformations pour chacune des jauges de la rosette pour les 3 cas de chargements.

Exploitation des mesures

Compléter (ou utiliser?) le script javascript suivant qui permet de faire facilement les calculs:
Voici le script final qui fonctionne
Calculer l'opérateur des déformations au point de mesure pour chaque cas de chargement.
Calculer l'opérateur des contraintes au point de mesure pour chaque cas de chargement (état de contraintes planes).
Calculer les directions principales et les contraintes principales pour chaque cas.
Tracer le cercle de Mohr des contraintes pour les 3 cas de chargements.
Trouver à partir du cercle de Mohr les directions principales et les contraintes principales.
Calculer les contraintes équivalentes de Tresca et de Von Mises pour chaque cas de chargement.
En utilisant le théorème de superposition, retrouver les résultats des cas de chargements combinés flexion-torsion à partir des autres mesures.
Calculer les contraintes tournées d'un angle de 45^o par rapport à l'axe x des jauges; ces contraintes tournées sont alors écrites dans une base (x',y') où x' est l'axe X de la poutre. Comparer ces résultats avec les contraintes obtenues par le modèle poutre.